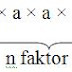Rabu, 08 Februari 2017

Soal Lingkaran Kelas VIII

04.50 Eva masyrofah Kelas VIII, Kuis, Lingkaran No comments

Kuis Lingkaran by ProProfs » Create your own Personality Quiz

Soal Bilangan Berpangkat dan Bentuk Akar Kelas IX

06.08 Eva masyrofah Bilangan Berpangkat dan Bentuk Akar, Kelas IX No comments

Kuis Bilangan Berpangkat dan Bentuk Akar » Quiz Created With ProProfs

BENTUK AKAR

05.56 Eva masyrofah akar pangkat, Bentuk akar, Kelas IX No comments

Standar Kompetensi : 5. Memahami sifat-sifat bilangan berpangkat dan bentuk akar serta penggunaannya dalam pemecahan masalah sederhana

Kompetensi Dasar :

5.1. Mengidentifikasi sifat-sifat bilangan berpangkat dan bentuk akar

5.2. Melakukan operasi aljabar yang melibatkan bilangan berpangkat bulat dan bentuk akar.

Tujuan Pembelajaran : Siswa dapat mengidentifikasi sifat-sifat bentuk akar dan melakukan operasi aljabar pada bentuk akar

A. Pengertian

Bentuk akar merupakan bentuk yang menyatakan bilangan berpangkat pecahan.

Contoh :

Jadi secara umum ditulis :

dibaca akar pangkat n dari a sama dengan a pangkat seper-n.

B. Sifat-sifat akar

Contoh:

$\sqrt{3^{2}\times 5^{2}}=\sqrt{3^{2}}\times \sqrt{5^{4}}$
$=3\times 5^{2}$

$\sqrt{27^{\frac{2}{3}}}=\sqrt{\left (3^{3} \right )^{\frac{2}{3}}}$
$=\sqrt{3^{2}}$

$\sqrt{\frac{32}{18}}=\sqrt{\frac{2\times 16}{2\times 9}}$
$=\frac{\sqrt{16}}{\sqrt{9}}$
$=\frac{4}{3}$

C. Operasi aljabar pada bentuk akar

Contoh:

$\sqrt{12}+\sqrt{27}-\sqrt{3}=2\sqrt{3}+3\sqrt{3}-\sqrt{3}$
$=4\sqrt{3}$

$5\sqrt{2}\times \sqrt{8}=5\sqrt{2}\times 2\sqrt{2}$
$=5\times 2\times \sqrt{2\times 2}$
$=5\times 2\times 2$

$\frac{\sqrt{24}}{\sqrt{18}}=\frac{2\sqrt{6}}{3\sqrt{2}}$

$=\frac{2}{3}{\sqrt{3}}$

Berikut ini video penyelesaian bentuk akar pada soal UN:

BILANGAN BERPANGKAT

00.51 Eva masyrofah Bilangan Berpangkat, Kelas IX, Pangkat No comments

Standar Kompetensi : 5. Memahami sifat-sifat bilangan berpangkat dan bentuk akar serta penggunaannya dalam pemecahan masalah sederhana

Kompetensi Dasar :

5.1. Mengidentifikasi sifat-sifat bilangan berpangkat dan bentuk akar

5.2. Melakukan operasi aljabar yang melibatkan bilangan berpangkat bulat

dan bentuk akar.

Tujuan Pembelajaran : Siswa dapat mengidentifikasi sifat-sifat bilangan berpangkat dan melakukan operasi pada bilangan berpangkat

A. Pengertian

Jika a Î R (bilangan real) dan n adalah bilangan bulat, maka bilangan aⁿ (dibaca a pangkat n) didefinisikan sebagai perkalian berulang a sebanyak n kali (faktor).

aⁿ disebut bilangan berpangkat, a disebut bilangan pokok, dan n disebut pangkat (eksponen).

B. Sifat-sifat bilangan berpangkat

Contoh:
1. $8^{\frac{1}{3}}+25^{\frac{1}{2}}-16^{\frac{3}{4}}=\left (2^{3} \right )^{\frac{1}{3}}+\left (5^{2} \right )^{\frac{1}{2}}-\left (2^{4} \right )^{\frac{3}{4}}$

2. $\left (5^{-2}\times 5^{5} \right )^{-1}=\left (5^{-2+5} \right )^{-1}$
   $=\left (5^{3} \right )^{-1}$
   $=5^{-3}$
   $=\frac{1}{5^{3}}$
   $=\frac{1}{125}$

3. $\left (\frac{8}{27} \right )^{\frac{2}{3}}=\left (\frac{2^{3}}{3^{3}} \right )^{\frac{2}{3}}$
   $=\frac{\left (2^{3} \right )^{\frac{2}{3}}}{\left (3^{3} \right )^{\frac{2}{3}}}$
   $=\frac{2^{2}}{3^{2}}$
   $=\frac{4}{9}$

4. Berdasarkan data BPS tahun 2010 jumlah penduduk pulau Jawa mencapai 130 juta jiwa (melalui proses pembulatan). Sedangkan luas pulau Jawa 130 x 10³ km². Berapakah kepadatan penduduk pulau jawa tahun 2010?

Jumlah penduduk = 130.000.000 jiwa

= 1,3 x 10⁸

Luas pulau Jawa = 130 x 10³ km²

= 1,3 x 10⁵

Kepadatan penduduk = Jumlah penduduk : Luas pulau Jawa

= 1,3 x 10⁸ : 1,3 x 10⁵

= 1 x 10³

= 1000 jiwa /km²

5. Dinda membeli flashdisk baru seharga Rp 85.000,00 dengan kapasitas 16 GB. Berapa byte kapasitas flashdisk Dinda yang bisa digunakan, jika dalam suatu flashdisk yang dapat digunakan adalah 95% dari kapasitas totalnya?

Pembahasan:

Kapasitas flashdisk 16 GB = 16 x 10⁹B

Kapasitas yang dapat digunakan = 95% x 16 x 10⁹B

= 95 x 16 x 10⁷B

= 1.520 x10⁷B

= 1,52 x 10¹⁰B

6. Massa bulan 7,3477 x 10²² kg. Massa Bumi sama dengan 81,3 massa bulan. Massa bumi adalah ....

Pembahasan:

Massa bumi = 81,3 x 7,3477 x 10²² kg

= 597,368 x 10²² kg

= 5,97368 x 10²⁴ kg

LUAS LINGKARAN

01.32 Eva masyrofah Kelas VIII, Lingkaran, Luas Lingkaran No comments

Standar Kompetensi : 4. Menentukan unsur, bagian lingkaran serta ukurannya

Kompetensi Dasar : 4.2 Menghitung keliling dan luas lingkaran

Tujuan Pembelajaran : Siswa dapat mengetahui rumus luas lingkaran dan menggunakannya.

MENEMUKAN NILAI PHI DAN KELILING LINGKARAN

00.32 Eva masyrofah Kelas VIII, Keliling Lingkaran, Lingkaran, Menemukan nilai phi No comments

Standar Kompetensi : 4. Menentukan unsur, bagian lingkaran serta ukurannya

Kompetensi Dasar : 4.2 Menghitung keliling dan luas lingkaran

Tujuan Pembelajaran:

1. Siswa dapat menemukan pendekatan nilai phi

2. Siswa dapat menemukan rumus keliling lingkaran

3. Siswa dapat menggunakan rumus keliling lingkaran

Siapkan benda-benda berbentuk lingkaran, kemudian ukurlah keliling dan diameternya. Isilah tabel berikut:

Kesimpulan apa yang kalian dapat?

Pada percobaan di atas kita mendapatkan:

$\pi =\frac{K}{d}$

Maka rumus keliling lingkaran :

$K=\pi d$

Contoh Soal

1. Diameter lingkaran 14 cm. Tentukan keliling lingkaran!

Diketahui : d = 14 cm

Ditanya : K

Jawab :

   $K=\pi d$
   $K=\frac{22}{7}\times 14cm$
   K = 44 cm

2. Keliling sebuah lingkaran 88 cm. Tentukan jari-jari lingkaran!

Diketahui : K = 88 cm

Ditanya : r

Jawab                :
   $K=\pi d$
    $88cm=\frac{22}{7}\times d$
   $d=\frac{7\times 88cm}{22}$
d = 28 cm
r = 14 cm

3. Sebuah roda dengan diameter 70 cm berputar 1000 kali. Tentukan panjang lintasan yang dilalui roda tersebut!

Diketahui : d = 70 cm

Banyak putaran roda = 1000

Ditanya : panjang lintasan roda

Jawab :
Panjang lintasan roda = Keliling roda x banyak putaran

$=\pi \times d\times n$
$=\frac{22}{7}\times 70cm\times 1000$
= 220.000 cm
= 2,2 km

UNSUR-UNSUR LINGKARAN

00.15 Eva masyrofah Kelas VIII, Lingkaran, Unsur-unsur lingkaran No comments

Standar Kompetensi : 4. Menentukan unsur, bagian lingkaran serta ukurannya

Kompetensi Dasar : 4.1 Menentu kan unsur dan bagian-bagian lingkaran

Tujuan Pembelajaran : Siswa dapat menyebutkan unsur-unsur dan bagian-bagian lingkaran

Lingkaran adalah bangun datar tempat kedudukan titik-titik (himpunan semua titik) yang berjarak sama terhadap sebuah titik tertentu. (A circle is the set of all points in a plane whose distance from a given point is a fixed constant length).

Belajar Matematika SMP

Meniti jalan, meraih asa, menjadi generasi harapan umat

Rabu, 08 Februari 2017

Soal Lingkaran Kelas VIII

Selasa, 07 Februari 2017

Soal Bilangan Berpangkat dan Bentuk Akar Kelas IX

Senin, 06 Februari 2017

BENTUK AKAR

Minggu, 05 Februari 2017

BILANGAN BERPANGKAT

Sabtu, 04 Februari 2017

LUAS LINGKARAN

MENEMUKAN NILAI PHI DAN KELILING LINGKARAN

UNSUR-UNSUR LINGKARAN

Popular Posts

Recent Posts

Categories

Blog Archive

Mengenai Saya

Formulir Kontak

Pengunjung

Recent

Comment

Subscribe

Label

Tags

Translate

Facebook

Featured Posts

Random Posts

Recent Posts

Popular Posts